Trigonometriezh sferek

An drigonometriezh sferek zo un teskad liammadennoù damheñvel ouzh re an drigonometriezh euklidian met gant kornioù ha pellderioù daveet war ur sferenn.

Ne c'heller ket implijout reolennoù boas an drigonometriezh euklidian ken ; da skouer ez eo brasoc'h somm kornioù un tric'horn lec'hiet war ur sferenn eget 180 derez hag dont a ra ar segmantoù eeunenn da vezañ gwaregoù kelc'hioù bras.

An tric'horn sferek[kemmañ | kemmañ ar vammenn]

.

Formulennoù kentañ[kemmañ | kemmañ ar vammenn]

Kenemglevioù[kemmañ | kemmañ ar vammenn]

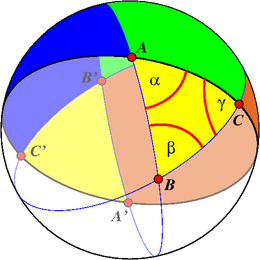
Bezet tri foent A, B ha C war ur sferenn evel taolennet gant ar figurenn amañ e-kichen, notet e vo a hirder kostez enep ar beg A hag α, a-wezhioù Â, korn (war gorreenn ar sferenn atav) an tric'horn er beg-se, hag evel se gant ar begoù all. Evit gwir e vo sellet ouzh an hirderioù a, b ha c evel kornioù el lodenn war-lerc'h, eleze ar c'hornioù is-stegnet war greizenn ar sferenn gant kostezioù an tric'horn (sellet ouzh an eil figurenn ; trohed ar sferenn eo ar c'horn 2π da skouer).

Formulenn ar c'hosinusoù ha liammadenn daouel[kemmañ | kemmañ ar vammenn]

Formulenn ar c'hosinusoù, roet gant François Viète e 1593 en e De Varorium^[1] zo unan eus liammadennoù pouezusañ an drigonometriezh sferek. Liammañ a ra hirder ur c'hostez ouzh re an daou gostez all hag ar c'horn etrezo :

\cos c=\cos a\,\cos b+\sin a\,\sin b\,\cos \gamma ~,

a zo arabat droukveskañ gant al liammadenn daouel, a gaver pa lakaer o foentoù polel e-lec'h an holl gelc'hioù bras el liammadenn-se :

\cos \gamma =-\cos \alpha \,\cos \beta +\sin \alpha \,\sin \beta \,\cos c~.

Meur a zoare a zo da brouiñ formulenn ar c'hosiniusoù. Unan anezho a zo ezteuler e meur a zoare liesad skalarel ar vektorioù a ere O, kreizenn ar sferenn, ouzh ar poentoù A ha B e-barzh ar spas euklidian endro. Unan all a vo displeget dre ar munud amañ dindan.

En degouezh dibar pa vez skouer an tric'horn e C e kaver :

\cos \,c=\cos \,a\cos \,b

;

klotañ a ra ar formulenn-se gant teorem Pythagoras evit an drigonometriezh sferek. Merzout a reer e kaver end-eeun en-dro teorem Pythagoras pa vez bihan a-walc'h an tric'horn evit lakaat o diorren bevennet a eil urzh e-lec'h ar c'hosinusoù.

Reiñ a ra tro formulenn ar c'hosinusoù da jediñ an hed etre daou boent A ha B war an Douar hervez o led hag o hed pergen. Evit se e lakaer ar poent C er pol norzh e doare ma vo a klokamant $\scriptstyle {\phi _{A}}$ , led A, b klokamant $\scriptstyle {\phi _{B}}$ , hini B, ha c an diferañs etre an hedoù $\scriptstyle {\Delta \lambda =\lambda _{B}-\lambda _{A}}$ . Kavout a reer war-eeun :

d_{AB}=Rc=R\arccos {\left(\sin \phi _{A}\sin \phi _{B}+\cos \phi _{A}\cos \phi _{B}\cos \Delta \lambda \right)}

.

Gallout a reer ivez skrivañ al liammadenn er stumm :

\cos \gamma ={\frac {\cos c-\cos a\,\cos b}{\sin a\,\sin b}}~.

Eus eztaolioù damheñvel evit cosα ha cosβ e teduer trede formulenn diaezez an drigonometriezh sferek (an div gentañ eo re ar c'hosinusoù hag ar sinusoù) :

\sin b\cos \alpha +\cos c\sin a\cos \beta =\sin c\cos a~.

Evit a sell ouzh al liammadenn daouel e c'heller he skrivañ

\cos c={\frac {\cos \gamma +\cos \alpha \,\cos \beta }{\sin \alpha \,\sin \beta }}~.

Formulenn ar sinusoù[kemmañ | kemmañ ar vammenn]

Merzout a reer diwar al liammadenn daouel meneget a-raok e vez dedermenet an tric'hornioù sferek gant o zri c'horn, ar pezh a zo disheñvel-bras diouzh degouezh an tric'hornioù euklidian (plaen). En tric'horn sferek ez eus un heñvelder peurglok (a zaouelder) etre hirder ar c'hostezioù hag ar c'hornioù er begoù. Skeudennet eo an heñvelder-se gant formulenn ar sinusoù :

{\frac {\sin a}{\sin \alpha }}={\frac {\sin b}{\sin \beta }}={\frac {\sin c}{\sin \gamma }}~,

pe c'hoazh :

\sin a:\sin b:\sin c=\sin \alpha :\sin \beta :\sin \gamma ~,

ar pezh a ranker kompren evel-henn : « emañ an tri c'hementad a gleiz er memes kenfeur gant an tri c'hementad a zehou (ar memes keñver etre daou gementad bennak a gleiz hag etre an daou gementad kenglot a zehou) ».

• Prouadur ar formulennoù kentañ

a, b ha c eo anvioù an hirderioù, A, B ha C eo anvioù ar poentoù, α, β ha γ eo anvioù kornioù an tric'horn sferek.

1) Sevel a reer daou zaveer ortonormet reizh R hag R dezho ar memes vektor kentañ, hag e doare ma vo A pol norzh sistem ar c'henurzhiennoù sferek stag ouzh an eil daveer, ha B pol su egile.

• Munudoù ar savadenn-se

Notañ a reer $R=(O,{\overrightarrow {i}},{\overrightarrow {j}},{\overrightarrow {k}})$ hag $R'=(O,{\overrightarrow {i'}},{\overrightarrow {j'}},{\overrightarrow {k'}})$ gant ${\overrightarrow {k}}={\overrightarrow {OA}},~{\overrightarrow {k'}}={\overrightarrow {OB}}~.$

Kemer a reer neuze :

{\overrightarrow {i}}={\overrightarrow {i'}}={1 \over \sin c}{\overrightarrow {k}}\wedge {\overrightarrow {k'}}={1 \over \sin c}{\overrightarrow {OA}}\wedge {\overrightarrow {OB}}~.

Deduiñ a reer alese :

{\overrightarrow {j}}={\overrightarrow {k}}\wedge {\overrightarrow {i}}={1 \over \sin c}[{\overrightarrow {OA}}\wedge ({\overrightarrow {OA}}\wedge {\overrightarrow {OB}})]~.

Gant formulenn al liesad vektorel doubl e teu :

{\overrightarrow {j}}={1 \over \sin c}((OA|OB){\overrightarrow {OA}}-||OA||^{2}{\overrightarrow {OB}})={1 \over \sin c}(\cos c~{\overrightarrow {OA}}-{\overrightarrow {OB}})~.

Er memes doare :

{\overrightarrow {j'}}={1 \over \sin c}[{\overrightarrow {OB}}\wedge ({\overrightarrow {OA}}\wedge {\overrightarrow {OB}})]={1 \over \sin c}({\overrightarrow {OA}}-\cos c~{\overrightarrow {OB}})~.

2) Ar cheñchamant daveer (eus R etrezek R) zo un troiadur er spas en-dro da ahel boutin an daou zaveer. Dre ma'z eo c ar c'horn etre

{\overrightarrow {OA}}

hag

{\overrightarrow {OB}}

e teduer ez eo ar matris tremen :

P={\begin{pmatrix}1&0&0\\0&\cos c&-\sin c\\0&\sin c&\cos c\end{pmatrix}}~.

3) Roet e vo bremañ kenurzhiennoù C en daveer R.

Merzout a reer ez eo b ar genledenn en daveer sferek, A e bol norzh, stag ouzh an daveer kartezian, tra m'eo α ar c'horn (er pol) etre ar vektor

-{\overrightarrow {j}}

hag an hanter-blaen a-blom (A,O,C), setu e talv an hedenn α-(π/2).

Deduiñ a reer alese ez eo kenurzhiennoù kartezian C en daveer kentañ (

^{[1,\alpha -{\pi  \over 2},b]}

eo e genurzhiennoù sferek) :

X={\begin{pmatrix}\sin b\sin \alpha \\-\sin b\cos \alpha \\\cos b\end{pmatrix}}~.

4) Er memes mod e vo roet kenurzhiennoù C en eil daveer R.

Ar wezh-mañ ez zo ar poent B ar pol norzh, a ar genledenn, ha β ar c'horn etre an hanter-blaen a-blom (B,O,C) hag ar vektor

{\overrightarrow {j'}}

, setu e talv an hedenn (π/2)-β.

Deduiñ a reer alese ez eo kenurzhiennoù kartezian C en eil daveer (

^{[1,{\pi  \over 2}-\beta ,a]}

eo e genurzhiennoù sferek) :

X'={\begin{pmatrix}\sin a\sin \beta \\\sin a\cos \beta \\\cos a\end{pmatrix}}~.

5) Formulenn ar cheñchamant diaz a skriver neuze :

{\begin{pmatrix}\sin b\sin \alpha \\-\sin b\cos \alpha \\\cos b\end{pmatrix}}=X=PX'={\begin{pmatrix}1&0&0\\0&\cos c&-\sin c\\0&\sin c&\cos c\end{pmatrix}}

{\begin{pmatrix}\sin a\sin \beta \\\sin a\cos \beta \\\cos a\end{pmatrix}}~.

En un taol e teduer alese formulenn ar sinusoù, trede formulenn ziazez an drigonometriezh sferek, ha formulenn ar c'hosinusoù :

{\begin{cases}\sin b\sin \alpha =\sin a\sin \beta \\\sin b\cos \alpha =\sin c\cos a-\cos c\sin a\cos \beta \\\cos b=\sin c\sin a\cos \beta +\cos c\cos a~.\end{cases}}

}}

Formmulennoù all[kemmañ | kemmañ ar vammenn]

Formulennoù an hanter-gornioù hag an hanter-gostezioù[kemmañ | kemmañ ar vammenn]

Bezet $\scriptstyle {s={\frac {1}{2}}(a+b+c)}$ , hanter-drohed an tric'horn. Neuze ez eo :

\tan ^{2}{\frac {\gamma }{2}}={\frac {\sin(s-a)\,\sin(s-b)}{\sin s\,\sin(s-c)}}

hag evit ar formulennoù daouel, gant $\scriptstyle {\sigma ={\frac {1}{2}}(\alpha +\beta +\gamma )}$ :

tan^{2}{\frac {c}{2}}=-{\frac {\cos \sigma \,\cos(\sigma -\gamma )}{\cos(\sigma -\alpha )\,\cos(\sigma -\beta )}}

.

N'eus somm ebet er formulennoù-se a liamm ur c'horn war greizenn ouzh tri c'hostez an tric'horn. Implijet e vezent stank evit ar jedadennoù pleustrek gant taolennadoù logaritmoù.

Formulennoù Gauss[kemmañ | kemmañ ar vammenn]

Bez' eo ${\frac {\cos {\frac {a+b}{2}}}{\cos {\frac {c}{2}}}}={\frac {\cos {\frac {\alpha +\beta }{2}}}{\sin {\frac {\gamma }{2}}}}$ ha ${\frac {\sin {\frac {a+b}{2}}}{\sin {\frac {c}{2}}}}={\frac {\cos {\frac {\alpha -\beta }{2}}}{\sin {\frac {\gamma }{2}}}}$ hag ivez ${\frac {\cos {\frac {a-b}{2}}}{\cos {\frac {c}{2}}}}={\frac {\sin {\frac {\alpha +\beta }{2}}}{\cos {\frac {\gamma }{2}}}}$ ah ${\frac {\sin {\frac {a-b}{2}}}{\sin {\frac {c}{2}}}}={\frac {\sin {\frac {\alpha -\beta }{2}}}{\cos {\frac {\gamma }{2}}}}~.$

Deduiañ a reer alese lezenn an tañjantoù e trigonometriezh sferek :

{\frac {\tan {\frac {a-b}{2}}}{\tan {\frac {a+b}{2}}}}={\frac {\tan {\frac {\alpha -\beta }{2}}}{\tan {\frac {\alpha +\beta }{2}}}}~.

Damheñvelderioù Napier[kemmañ | kemmañ ar vammenn]

Kavet e vezont dre genstrollañ formulennoù Gauss div-ha-div :

$\tan {\frac {c}{2}}\cos {\frac {\alpha -\beta }{2}}=\tan {\frac {a+b}{2}}\cos {\frac {\alpha +\beta }{2}}$
$\tan {\frac {c}{2}}\sin {\frac {\alpha -\beta }{2}}=\tan {\frac {a-b}{2}}\sin {\frac {\alpha +\beta }{2}}$
$\cot {\frac {\gamma }{2}}\cos {\frac {a-b}{2}}=\tan {\frac {\alpha +\beta }{2}}\cos {\frac {a+b}{2}}$
$\cot {\frac {\gamma }{2}}\sin {\frac {a-b}{2}}=\tan {\frac {\alpha -\beta }{2}}\sin {\frac {a+b}{2}}$

Gorread an tric'horn sferek[kemmañ | kemmañ ar vammenn]

Anavezet eo e saozneg dindan an anv formulenn Girard.

En un doare heverk e jeder aes-kenañ gorread an tric'horn sferek diwar e tri c'horn : kevatak-rik eo gant e « ziouer euklidianded » (diferañs etre somm kornioù an tric'horn ha π liesaet dre garrez R, skin ar sferenn. Setu :

S=({\hat {A}}+{\hat {B}}+{\hat {C}}-\pi )R^{2}=R^{2}\varepsilon

Evezhiadenn :ε zo ur c'horn solut a vez eztaolet e steradian (pa vez eztaolet $^{{\hat {A}},{\hat {B}}}$ ha $^{\hat {C}}$ e radian). Ur brouadenn diazez a c'heller ober e teir fazenn^[2].

a) Didroc'hañ e reer ar sferenn e peder "gwerzhid" gant daou blaen diametrel evel er figurenn amañ e-kichen. Galloud a reer jediñ gorread pep gwerzhid. Kenfeurel eo ar gorread gant Â, ar c'horn er poent A etre an daou blaen. Gorread ar sferenn a-bezh a gaver gant ar c'horn 2π ; kevatal eo gant 4πR².

Setu ez eo kevatal gorread ar werzhid gant :

{\frac {\hat {A}}{2\pi }}4\pi R^{2}=2{\hat {A}}R^{2}

.

b) Termenet eo an tric'horn sferek gant tri flaen a droc'h ar sferenn e daouzek gwerzhid. Teir anezho a endalc'h an tric'horn ABC, ha teir all, simetrek d'ar re gentañ, a endalc'h an tric'horn A'B'C' a zo enep dezhañ ez diametrel ha kevatal e c'horread eta. Gant ar c'hwec'h gwerzhid-se e c'holoer ar sferenn a-bezh, met teir gwezh eo bet goloet pep hini eus an tric'hornioù ABC hag A'B'C'. Pa sommer gorreadoù ar c'hwec'h gwerzhid-se e kaver gorread ar sferenn kresket eus peder gwezh T, gorread an tric'horn.

c) Da lavaret eo : $^{2(2{\hat {A}}R^{2}+2{\hat {B}}R^{2}+2{\hat {C}}R^{2})=4\pi R^{2}+4T}$ .

Deduiñ a reer alese neuze :

^{T=({\hat {A}}+{\hat {B}}+{\hat {C}}-\pi )R^{2}}

Dizoloet e voe ar formulenn-se gant Thomas Harriot hep bezañ embanet ha roet e voe evit ar wezh kentañ gant Albert Girard war-dro 1625.

Formulenn l'Huilier[kemmañ | kemmañ ar vammenn]

Damheñvel ar formulenn-se ouzh formulenn Heron a jed gorread an tric'hornioù euklidian hervez e gostezioù. Ober a ra ar memes tra gant an tric'hornioù sferek :

\tan {\frac {s}{2}}\tan {\frac {s-a}{2}}\tan {\frac {s-b}{2}}\tan {\frac {s-c}{2}}=\tan ^{2}{\frac {\varepsilon }{4}}

(degas a reer soñj ez eus bet graet s=(a+b+c)/2 eus an hanter-drohed).

Un damsell war an istor[kemmañ | kemmañ ar vammenn]

Degaset ez eus bet kalz d'an drigonometriezh, ha d'an drigonometriezh sferek pergen, gant an astronomourien ha matematikourien c'hresian Hipparc'hos Nikaia^[3] ha Menelaos Aleksandria, met ivez gant matematikourien Persia hag India. En o zouez emañ Al Biruni, Abu Nasr Mansur ha Bhāskara II. War a seblant e voe skrivet ar studiadenn gentañ war an drigonometriezh sferek war-dro 1060 gant Al-Jayyani (en), ur matematikour eus Andalouzia a oa dindan beli ar vuzulmaned da neuze.

Implijoù[kemmañ | kemmañ ar vammenn]

Jediñ kenurzhiennoù :

en astronomiezh, evit ar cheñchamantoù stag ouzh ar reizhiadoù diseurt a genurzhiennoù-korn : deklinadur, troad, korn-eur, azimut hag hed-zenit (pe uhelder) ;
e douaroniezh (ledred hag hedred) ;
en optik evit implijout sferenn Poincaré ;
e stadegouriezh war sferenn ikonografiezh ar c'horreladennoù.

Notennoù ha daveoù[kemmañ | kemmañ ar vammenn]

↑ (fr) Michel Chasles : Mémoires sur les questions proposées par l'Académie royale des sciences de Bruxelles pajenn 54.
↑ (fr) Un nebeud displegadennoù ouzhpenn a vo kavet e lec'hienn ar Palais de la découverte
↑ (fr) Œuvres complètes de François Arago. François Arago, levrenn 3, pajenn 158 (Gide, Pariz - 1855).