Roudad RC

Ur roudad RC a zo ur roudad tredan, savet gant ur resistañs hag ur c'hondensatour a-steud pe en diroud. Pa 'z eo a-steud, ar roudad RC a servij da sevel siloù tredan pas-izel pe pas-uhel. Digemm amzer $\tau$ ur roudad RC a zo roet gant lieskement talvoud an daou elfenn a sav ar roudad.

Roudad a-steud

Roudad RC a-steud

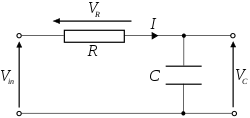
Fonksionoù trañsfer

Bezet $Z_{C}(\omega )$ impedañs ar c'hondensatour :

$Z_{C}(\omega )={\frac {1}{jC\omega }}$

Ar voltadur e bonnoù ar resistañs pe ar c'hondensatour a c'hell bezañ jedet o kemer ar roudad evel ur ranner voltadur nann karget :

$V_{C}(\omega )={\frac {Z_{C}(\omega )}{Z_{C}(\omega )+R}}V_{in}(\omega )={\frac {1}{1+jRC\omega }}V_{in}(\omega )$

$V_{R}(\omega )={\frac {R}{Z_{C}(\omega )+R}}V_{in}(\omega )={\frac {jRC\omega }{1+jRC\omega }}V_{in}(\omega )$.

Notennet eo $H_{C}$ ar fonksion trañsfer bet o kemer ar voltadur e bonnoù ar c'hondensatour evel voltadur mont er-maez hag $H_{R}$ ma vez implijet an hini e bonnoù ar resistañs. $H_{C}$ ha $H_{R}$ a vez kavet a-drugarez da eztaoladennoù $V_{C}$ ha $V_{R}$ :

$H_{C}(\omega )={V_{C}(\omega ) \over V_{in}(\omega )}={1 \over 1+jRC\omega }$

$H_{R}(\omega )={V_{R}(\omega ) \over V_{in}(\omega )}={jRC\omega \over 1+jRC\omega }$

Evit un dipol, tu zo skrivañ ar fonksion trañsfer dindan ar stumm $H(\omega )=Ge^{j\varphi }\,$ , lec'h 'm eo $G\,$ gounid an dipol ha $\varphi \,$ e fazenn. Neuze :

$H_{C}(\omega )=G_{C}e^{j\varphi _{C}}$

gant

$G_{C}={\frac {1}{\sqrt {1+\left(\omega RC\right)^{2}}}}$

ha

$\varphi _{C}=\arctan \left(-\omega RC\right)$

Heñvel evit $H_{R}$ :

$H_{R}(\omega )=G_{R}e^{j\varphi _{R}}$

gant

$G_{R}={\frac {\omega RC}{\sqrt {1+\left(\omega RC\right)^{2}}}}$

ha

$\varphi _{R}=\arctan \left({\frac {1}{\omega RC}}\right)$,

Analiz frekañsel

Lechioù Bode $H_{C}$

Gant un analiz frekañsel eus ar roudad ez eus tu kavout peseurt frekañsoù a zo restaolet pe asantet gant ar sil. Evit ar frekañsoù izel en deus $H_{C}$ ur modul tost eus unan hag ur fazenn tost eus zero. Seul vui ma gresk ar frekañs, seul izeloc'h e vo ar modul evit tennañ war-zu zero hag e fazenn $-\pi /2$. Er c'hontrol, $H_{R}$ en deus ur modul tost eus zero war frekañsoù izel hag ur fazenn tost eus $\pi /2$ ha pa gresk ar frekañs e tenn e modul war-zu unan hag e fazenn war-zu zero.

Pa $\omega \to 0$ :

$G_{C}\to 1$ et $\varphi _{C}\to 0$.

$G_{R}\to 0$ et $\varphi _{R}\to 90^{\circ }=\pi /2$.

Pa $\omega \to \infty$ :

$G_{C}\to 0$ et $\varphi _{C}\to -90^{\circ }=-\pi /2$

$G_{R}\to 1$ et $\varphi _{R}\to 0$.

Evel-se, pa z'eo mont er-maez ar sil kemeret war ar c'hondensatour an emzalc'h a zo eus an doare filtr pas-izel : ar frekañsoù uhel a zo digreskaet hag ar frekañsoù uhel a dremen. Ma 'z eo ar mont er-maez kemeret war ar resistañs eo ar c'hontrol hag ar roudad en deus un emzalc'h sil pas-uhel.

Frekañs troc'hañ $f_{c}$ ar roudad a spis ar bevenn da 3dB etre ar frekañsoù izelet hag ar re n'int ket a zo par da :

$f_{c}={\frac {1}{2\pi RC}}$ (e Hz)

Analiz amzeriel

Evit abegoù simpladur, an analiz amzeriel a zo graet oc'h implijout treuzfurmat Laplace p. O goulakaat ez eo sujet ar roudad d'ur voltadur krannelek eus ampled V e mont e-barzh ( $V_{in}=0\,$ evit $t=0\,$ ha $V_{in}=V\,$ mod-all) :

$V_{in}(p)={\frac {V}{p}}$

$V_{C}(p)=H_{C}(p)V_{in}(p)={\frac {1}{1+pRC}}{\frac {V}{p}}$

$V_{R}(p)=H_{R}(p)V_{in}(p)={\frac {pRC}{1+pRC}}{\frac {V}{p}}$.

Kontrol treuzfurmat Laplace eus an eztaoladennoù-se a ro :

$V_{C}(t)=V\left(1-e^{-t/RC}\right)$

$V_{R}(t)=Ve^{-t/RC}\,$.

D'ar mare-se, ar c'hondensatour a karg hag ar voltadur d'e bonnoù a tenn war-zu V, pa z' eo an hini e bonnoù ar resistañs o tennañ war-zu 0.

Ar roudad RC en deus un digemm amzer, peurliesañ notennet $\tau =RC\,$, o tiskouezhout an amzer ma gemer ar voltadur evit ober 63% ($1-e^{-1}$) eus ar variadur ret evit tremen eus e talvoud inisial d'e talvoud final.

Tu zo ivez deverañ an eztaoladennoù-se eus an kevatalennoù diferañsial o diskrivañ ar roudad :

${\frac {V_{in}-V_{C}}{R}}=C{\frac {dV_{C}}{dt}}$

$V_{R}=V_{in}-V_{C}\,$.

An diskoulmoù a zo dres ar memes reoù eget ar re tapet gant treuzfurmat Lapalce.

Integrer

D'ur frekañs uhel, da lâret eo ma $\omega >>{\frac {1}{RC}}$, ar c'hondensatour n'eus ket amzet kargañ hag ar voltadur d'e bonnoù a chom izel.

Evel-se :

$V_{R}\approx V_{in}$

ha fonder ar roudad a zo neuze kevatal da :

$I\approx {\frac {V_{in}}{R}}$.

Evel m'eo,

$V_{C}={\frac {1}{C}}\int _{0}^{t}Idt$

kavet e vez :

$V_{C}\approx {\frac {1}{RC}}\int _{0}^{t}V_{in}dt$ .

Ar voltadur e bonnoù ar c'hondensatour a integr neuze ar fonksion mont e-barzh hag ar roudad en deus un emzalc'h orjaladenn integrer, da lâret eo evel ur sil pas-izel.

Derever

D'ur frekañs izel, da lâret eo ma $\omega <<{\frac {1}{RC}}$, ar c'hondensatour en deus amzer kargañ tost penn-da-benn.

Neuze,

$I\approx {\frac {V_{in}}{1/j\omega C}}$

$V_{in}\approx {\frac {I}{j\omega C}}\approx V_{C}$

Bremañ,

$V_{R}=IR=C{\frac {dV_{C}}{dt}}R$

$V_{R}\approx RC{\frac {dV_{in}}{dt}}$.

Ar voltadur e bonnoù ar resistañs a zerev neuze ar voltadur mont e-barzh hag ar roudad en deus un emzalc'h orjaladenn derever, da lâret eo evel ur sil pas-uhel.

Fonnder

Fonnder an tredan a zo ar memes hini e pep-lec'h er roudad, dre m'eo ur roudad a-steud :

$I(\omega )={\frac {V_{in}(\omega )}{R+Z_{C}}}={jC\omega \over 1+jRC\omega }V_{in}(\omega )$

Respont luskadenn

Ar respont luskadenn a zo amgin treuzfurmat Laplace eus ar fonksion trañsfer a glot ha diskouez a ra respont ar roudad d'ul luskadenn. Evit ar c'hondensatour :

$h_{C}(t)={1 \over RC}e^{-t/RC}u(t)={1 \over \tau }e^{-t/\tau }u(t)$

lec'h m'eo $u(t)\,$ fonksion Heaviside ha $\tau \ =\ RC$ a zo an digemm amzer.

Evit ar resistañs :

$h_{R}(t)=-{1 \over RC}e^{-t/RC}u(t)=-{1 \over \tau }e^{-t/\tau }u(t)$

Roudad en diroud

Roudad RC en diroud

Ar roudad RC en diroud a zo peurvuiañ gant un interset bihannoc'h eget ar roudad RC a-steud : ar voltadur mont er-maez a zo kevatal d'ar voltadur mont e-barzh, ne c'hell bezañ implijet evel sil nemet ma 'z eo luget d'un andon tredan.

Ar fonnder en daou dipol a zo :

$I_{R}={\frac {V_{in}}{R}}$

$I_{C}=j\omega CV_{in}\,$ .

Ar red-tredan er c'hondensatour a zo difazet eus 90° e-keñver ar red-tredan mont e-barzh (hag ar resistañs).

Sujet d'ur voltadur krannelek, ar c'hondensatour en em karg en un doare prim hag a c'hell bezañ kemmeret evet roudad digor, ar roudad en deus neuze un emalc'h resistañs.

Gwelet ivez

• Roudad tredan
• Roudad LC
• Roudad RL
• Roudad RLC