Korn (mentoniezh)



Ur c'horn zo ur stumm mentoniezh dezvonnet gant div eeunenn gengej.
Notenniñ ar c'hornioù
[kemmañ | kemmañ ar vammenn]Alies a-walc'h e vez notennet ar c'hornioù war-bouez lizherennoù c'hresianek (α, β, γ, δ, θ, φ, ...). Ne vez ket implijet al lizherenn π koulskoude, rak talvezout a ra al lizherenn-se evit an niver dija. Ober a reer ivez gant lizherennoù munut latin (a, b, c, ...), hag a-wezhioù gant pennlizherennoù latin evit al liestuegoù.
Gant an tri foent o zermen e c'haller notenniñ ar c'hornioù c'hoazh. Da skouer, ar c'horn termenet gant an tri foent A, B ha K a zo e veg en A a c'haller notenniñ ∠BAK pe . Pa ne vez riskl ebet e vefe droukvesket e c'haller ober gant ar beg ar c'horn hepken (en degouezh-mañ : "korn A").
Ar c'hornioù hervez o digoradur
[kemmañ | kemmañ ar vammenn]Ar c'hornioù a-hiniennoù
[kemmañ | kemmañ ar vammenn]An daouadoù kornioù
[kemmañ | kemmañ ar vammenn]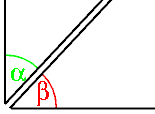

Un nebeud daouadoù kornioù a zo par o sammad d'ur c'horn heverk :
- ar c'hornioù serzhus a zo par o sammad d'ar c'horn serzh (1/4 tro, 90°, pe radian),
- ar c'hornioù skladus a zo par o sammad d'ar c'horn sklat (1/2 dro, 180°, pe radian),
- ar c'hornioù leunius a zo par o sammad d'ar c'horn leun (2 dro, 360°, pe 2 radian).
Un nebeud daouadoù kornioù a zo par o diforc'h d'ur c'horn heverk :
- ar c'hornioù gourzhskladus a zo par o diforc'h d'ar c'horn sklat (1/2 dro, 180°, pe radian).
An daouadoù kornioù dezvonnet gant eeunennoù kengej
[kemmañ | kemmañ ar vammenn] |
 |
E-touez an daouadoù kornioù dezvonnet gant eeunennoù kengej emañ :
- ar c'hornioù kefin, dezvonnet pep hini gant un hevelep eeunenn ha gant un eeunenn disheñvel,
- ar c'hornioù ilgroaz, dezvonnet gant an hevelep div eenenn, met lec'hiet a bep tu eus o foent kengej.
Par eo ar c'hornioù ilgroaz an eil d'egile.
Daou gorn kefin dezvonnet gant div eeunenn gengej a vez skladus atav.
Ar c'hornioù a denn d'un eeunenn dreuz
[kemmañ | kemmañ ar vammenn]
Ar c'hornioù a-hiniennoù
[kemmañ | kemmañ ar vammenn]Daou zoare kornioù a zo dezvonnet gant pep hini eus an div eeunenn hag an eeunenn dreuz :
- ar c'hornioù diabarzh a zo etre an div eeunenn,
- ar c'hornioù diavaez a zo en eil tu hag egile eus an div eeunenn.
An daouadoù kornioù
[kemmañ | kemmañ ar vammenn]Meur a zaouad kornioù a c'haller termeniñ :
- ar c'hornioù kenheuilh a zo kornioù diabarzh en hevelep tu eus an eeunenn dreuz,
- ar c'hornioù keñverek a zo kornioù diabarzh ha diavaez en hevelep tu tu eus an eeunenn dreuz,
- ar c'hornioù keñverenebek a zo kornioù diabarzh pe diavaez a bep tu eus an eeunenn dreuz,
- ar c'hornioù keñverenebek diabarzh a zo kornioù diabarzh a bep tu eus an eeunenn dreuz,
- ar c'hornioù keñverenebek diavaez a zo kornioù diavaez a bep tu eus an eeunenn dreuz.
Pa vez kenstur an div eeunenn e vez skladus ar c'hornioù kenheuilh, e vez par ar c'hornioù keñverek hag e vez par ar c'hornioù keñverenebek ivez.
Ar c'hornioù a denn d'al liestuegoù
[kemmañ | kemmañ ar vammenn]Ar c'hornioù a-hiniennoù
[kemmañ | kemmañ ar vammenn]
Daou zoare kornioù a denn d'al liestuegoù rez :
- ar c'hornioù diabarzh eus ul liestueg rez, dezvonnet gant daou du eus al liestueg hag a ya d'ober ur beg anezhañ,
- ar c'hornioù diavaez eus ul liestueg rez, dezvonnet gant unan eus e duioù hag astenn unan all hag a ya d'ober ur beg gantañ.
Jediñ a c'haller sammad kornioù diabarzh ul liestueg rez n tu. E radianoù, , hag e derezioù, pe . Alese e c'haller jediñ korn diabarzh ul liestueg keitkornek n tu. E radianoù ez eo par da , hag e derezioù da pe da .
Jediñ a c'haller ivez kornioù diavaez ul liestueg reoliek rez n tu. E radianoù ez int par da , hag e derezioù da .
Ur c'horn all a c'haller menegiñ evit al liestuegoù reoliek rez :
- ar c'horn kreizet, dezvonnet gant div eunenn hag a dremen dre greiz al liestueg ha dre bep hini eus an daou veg a ya d'ober un tu eus al liestueg.
Jediñ a c'haller kornioù kreizet ul liestueg reoliek rez n tu. Par eo an n korn kreizet, ha par eo o sammad da π radian pe da 360° E radianoù ez eo par ar c'hornioù kreizet da , hag e derezioù da . Par int d'ar c'hornioù diavaez neuze.
An daouadoù kornioù
[kemmañ | kemmañ ar vammenn]
Daou gorn kenheuilh eus ul liestueg rez a zo daou gorn diabarzh eus al liestueg-se dezvonnet gant un hevelep tu hag un tu disheñvel anezhañ.
Daou gorn ragenep eus ur pevarzueg rez a zo daou gorn ha n'int ket dezvonnet gant un hevelep tu. Daou gorn ragenep par a zo en ur sarpant-nij, ha par eo ar c'hornioù eus pep daouad kornioù ragenep en ur c'hensturieg.
Ar c'hornioù a denn d'ar c'helc'hioù
[kemmañ | kemmañ ar vammenn]
Ur c'horn kaeet a zo dezvonnet gant div eeunenn a zo kengej en ur poent eus ur c'helc'h hag a gej ar c'helc'h-se en ur poent all.
Ur c'horn kreizet a zo dezvonnet gant div eeunenn a zo kengej e kreiz ur c'helc'h.
Ur c'horn kreizet a zezvonn an hevelep gwarenn gelc'h hag ur c'horn kaeet a zo par da zaougement hemañ diwezhañ.